Graph 에 대한 개념정리 - 4
주제 : Activity Network
Graph의 응용에서는 'activity network'라는 구조가 존재하는 데 이에 대해서 알아보는 시간을 가지도록 하겠다. Activity Network은 다음과 같이 크게 두 종류로 나눠볼 수 있다.
1. AOV (= Active On Vertex)
2. AOE (= Active On Edge)
1. AOV (= Activity On Vertex) Network
1. A directed graph
2. vertex : 어떤 task나 activity를 의미
3. edge : activity 간의 선후관계(precedence relation)를 의미
2. AOE (= Activity On Edge) Network
1. Edge가 Activity를 의미하며, vertex는 시작과 종료 event를 의미
그래서 각각에 대해서 조금 더 자세히 정리해보도록 하겠다.
1. AOV (= Activity On Vertex) Network
이는 다음 조건을 만족하는 directe graph를 의미한다.
1. vertex = 어떤 task나 activity를 의미
2. Edge = activity 간의 선후관계 (precedence relation)를 의미
아래의 자료를 통해서 확인할 수 있듯이, 특정 전공에 대한 교과과정 체계를 표현하는 데 필요한 선수관계의 개념을 AOV Network를 통해서 표현하는 것이 가능하다.

Topological Sort
Topological Order를 찾는 문제

AOV Network의 전형적인 응용은 바로 Topological Sort 이다. 위에서 언급한 것처럼 Topological Sort 는 Topological Order를 찾는 문제에 해당하며, Topological Order는 아래와 같은 절차를 통해서 찾을 수 있다.
모든 vertex가 없어질 때까지 다음을 반복한다.
1. predecessor 가 없는 vertex를 선택 (predecessor는 위의 예시에서 선수과목을 의미함)
2. 해당 vertex와 그 vertex의 outgoing edge 를 삭제
만약, 위와 같이 교과과정 이수체계를 AOV로 나타냈다면 그 선수체계 조건을 만족하며서 교과과정을 이수하는 순서를 결정하는 것을 Topological Sort라고 기억하면 된다. 즉, 전체에서 선수과계에 대한 체계를 저해받지 않고 모든 강의를 이수할 수 있는 그 squence를 찾고 결정하는 것이 Topological Sort라고 이해할 수 있을 것이다. Topological Sort는 Graph의 종류와 그 구성방식에 따라서 한 가지가 아닌 다양한 결과가 나올 수 있다 (즉, 위에서 나온 예시는 솔루션 중 하나일 뿐이니 절대적인 솔루션이 아니라는 의미이다).
단, 모든 vertex가 선택되지 않는 경우, 이는 cycle이 존재함을 뜻한다. 실제로 교과과정에서 Cycle이 존재하는 것을 말이 되지 않는 상황이기 때문이다. AOV Network는 일반적으로 Cycle을 가지고 있지 않기 때문에 이러한 문제점은 발생하지 않는다.
AOE (= Activity On Edge) Networks
edge가 activity의 의미를 가지며, 이 각각의 edge는 weighted edge (예 : 소요시간) 에 해당한다.
아래와 같은 graph가 있다고 가정해보도록 하겠다. 아래의 graph를 보면 start, finish vertex가 존재하는 것을 확인할 수 있는데, 이는 각각 어떠한 작업을 처리하는 프로세스에 대해서 시작과 종료를 의미하는 것이며, 그렇기 때문에 start에서 end로의 direction 흐름은 어떤 작업이 처리되는 프로세스를 의미한다고 이해할 수 있다.
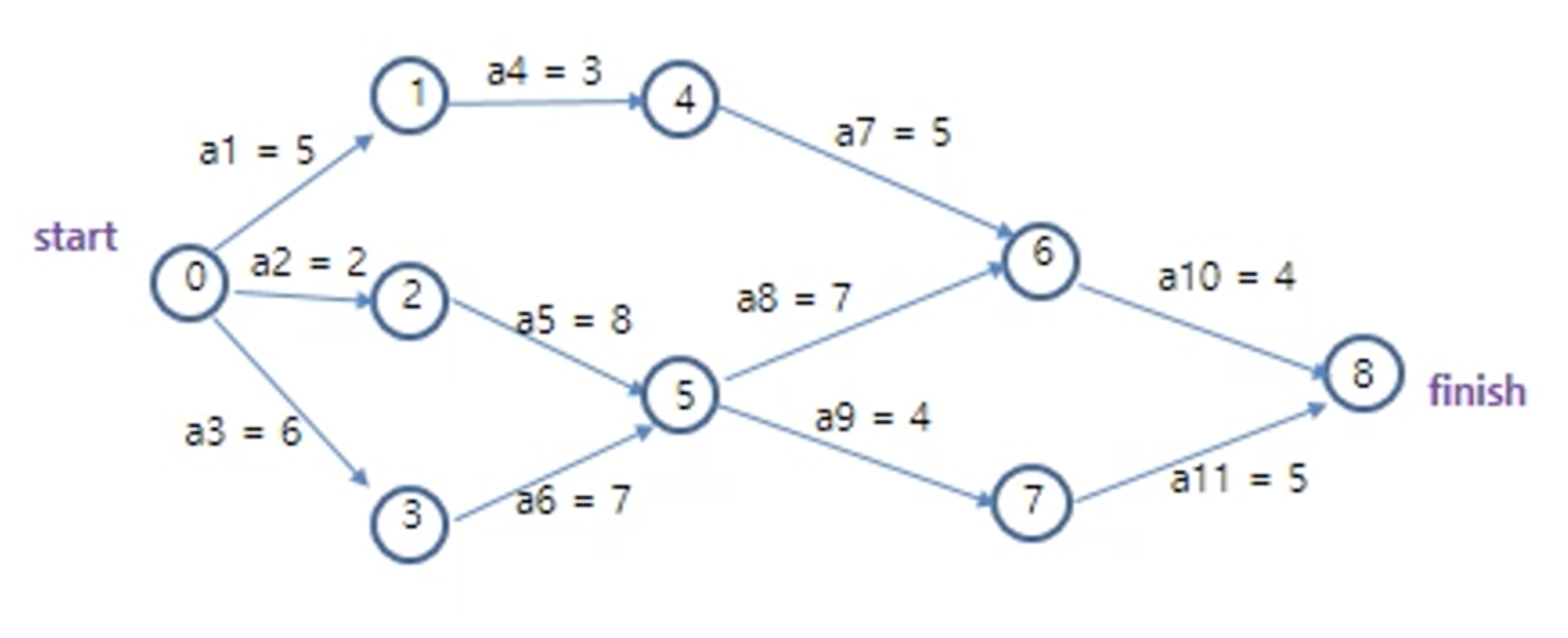
위의 그래프에서 각각의 edge (a1, a2, a3, ...) 는 각각 어떠한 일을 처리하는 동작을 의미하며, 이 edge에 할당된 weight 값은 해당 작업을 처리하는 데 걸리는 시간을 의미한다. 그래서 이를 잘 보면 위의 graph는 digraph이기 때문에 a1이 완료된 뒤에 a4를 수행할 수 있고, a2를 수행한 뒤에 a5를 수행할 수 있는 일종의 "프로젝트 공정"을 표현하는 것이라고 이해할 수 있다.
그래서 AOE는 어떠한 "작업 프로젝트 공정"을 표현하고 분석하는 데 유용하게 사용될 수 있는 데이터 구조에 해당한다.
AOE를 우리는 어떠한 작업프로젝트의 관점에서 다양하게 응용하는 것이 가능한데, 특히 다음 3가지가 프로젝트 공정을 표현하고 분석함에 있어서 많이 활용된다.
1. Critical Path - 프로젝트의 진행에 있어서 전체 성능에 영향을 주는 부분은 어디인 가?
2. Earliest Path - 어떤 작업이 가장 빠르게 시작될 수 있는 시각
3. Latest Path - 어떤 작업이 적어도 반드시 시작되어야 하는 시각
그렇다면 이 각각에 대해서 하나씩 알아보도록 하자.
Critical Path
1. Start vertex부터 finish vertex 까지의 longest path
2. 전체 성능에 영향을 주는 activities
3. 프로젝트의 performance를 평가하여 발생하는 bottleneck(병목)을 알아냄
여기서의 핵심은 Critical path가 아닌 부분에서 아무리 작업 시간을 개선한다고 하더라도 결과적으로 critical path의 처리 결과와 함께 연동되어야 한다면 전체적인 성능은 개선되지 않는다. 즉, critical path에 대한 성능을 개선해야만 전체 프로젝트에 대한 성능을 개선할 가능성이 높다는 것이다. 여기서 개선할 수 있다가 아닌 "가능성이 높다"라고 표현하는 이유는 graph 상에서 critical path가 1개가 아닌 2개 이상이 될 가능성이 존재하기 때문이다. 그렇기 때문에 critical path에 대한 성능을 개선한다고 해서 항상 전체 프로젝트의 성능 개선을 보장할 수는 없지만, 그러할 가능성을 매우 높여주게 된다.

Earliest Start Time
해당 activity가 시작될 수 있는 가장 빠른 시간

만약 아래의 예시에서 a7의 작업자가 자신이 가장 빨리 일을 시작할 수 있는 시간을 생각해본다고 한다면, 자신보다 이전 단계에 있는 작업들이 모두 재시간에 맞춰서 작업을 끝낸 5+3 = 8 만에 작업을 시작할 수 있다는 판단을 할 수 있게 된다. 그래서 a7에 대한 earliest start time은 8이 된다.
a8의 경우에는 a2, a5를 통해 수행되는 작업과, a3, a6를 통해 수행되는 작업이 모두 완료되어야 a8을 수행할 수 있기 때문에 a8에 대한 earliest start time은 6+7 = 13 이 된다. 결국은 해당 edge에 이르는 path 중에서 가장 긴 시간이 해당 edge에 대한 earliest start time 이 된다고 기억하면 된다.
동일한 논리를 적용하면 a11에 대한 earliest start time은 6+7+4 = 17 이 된다.
즉, earliest start time은 "최대한 빠르면 언제 해당 작업을 수행할 수 있음을 의미하게 된다."
Latest Start Time
해당 activity가 적어도 반드시 수행되어야 하는 가장 늦은 시간
전체 공정시간에서 영향을 주지 않는 작업들은 critical path 작업들이 작업을 완료하는 기한 범위 내에서 적절히 자신의 작업을 연기하는 것이 가능하다. 즉, a8에 이르는 path (a2->a5와 a3->a6)를 고려해본다고 할 때 a3, a6에 대한 path가 13의 시간이 필요하고, a2, a5에 대한 path가 10의 시간이 필요하기 때문에 만약 a2를 수행한 뒤에 3의 시간을 대기한 후 5의 시간부터 a5를 수행한다고 하더라도 이는 전체 작업시간을 지연시키지 않는다. 즉, a5에 대한 Latest Start Time에 대한 값을 5가 되는 것이다.

그래서 a7에 대해서 고려해보면, a7에 대한 처리결과가 a10을 수행함에 있어서 필요하기 때문에 event vertex6에 이르는 path들 중 가장 긴 소요시간을 계산해보면 6+7+7 = 20이 된다. 따라서 a7이 5의 시간을 필요로하기 때문에 a7이 20-5 = 15에만 시작된다면 전체 성능에 영향을 미치지 않음을 계산해볼 수 있다. 따라서 위의 graph에서 a7의 latest start time은 15가 된다.
a8의 경우에는 마찬가지로 a10을 처리하기 하는 데 그 결과가 필요하기 때문에 마찬가지로 20-7 = 13 에만 시작한다면 전체 성능에 영향을 미치지 않음을 계산해볼 수 있다. 따라서 위의 graph에서 a8의 latest start time은 13이 된다.
a11의 경우에는 a10의 결과와 함께 처리가 되는 데 a10이 처리되는 데 걸리는 시간이 6+7+7+4 = 24이기 때문에 적어도 a11이 24-5= 19에는 실행되어야 전체 프로젝트의 성능에 영향을 미치지 않고 작업을 수행할 수 있게 된다.
즉, latest start time은 "적어도 반드시 이 시간에는 해당 작업을 수행해야 함"을 의미한다.
따라서, 정리해보면 AOE Network에서는 전체 Network가 어떠한 공정 프로세스에 필요한 작업들과 소요시간, 그리고 그 선후관계를 표현한 것이라면 critical path를 구함으로써 전체 성능에 영향을 주는 부분이 어디인가를 알아낼 수 있고, 각 공정에 대해서 최대한 빨리 시작할 수 있는 시간, 적어도 반드시 시작해야하는 시간들을 earliest start time, latest start time을 분석함으로써 알아낼 수 있다.
특히, crtical path에 속하는 모든 작업은 earliest start time과 latest start time이 동일한 것을 알 수 있다. 즉, 예정대로 시간내에 작업을 수행해야 전체 수행시간에 영향을 미치지 않게 된다.
'Computer Science > 알고리즘' 카테고리의 다른 글
| 유클리드 호제법 (Euclidean-algorithm) (0) | 2023.06.07 |
|---|---|
| Greedy Algorithm (0) | 2022.07.11 |
| Graph에 대한 개념정리 - 3 (0) | 2021.05.21 |
| Graph에 대한 개념정리 - 2 (0) | 2021.05.21 |
| Graph에 대한 개념정리 - 1 (0) | 2021.05.21 |
댓글
이 글 공유하기
다른 글
-
유클리드 호제법 (Euclidean-algorithm)
유클리드 호제법 (Euclidean-algorithm)
2023.06.07 -
Greedy Algorithm
Greedy Algorithm
2022.07.11 -
Graph에 대한 개념정리 - 3
Graph에 대한 개념정리 - 3
2021.05.21 -
Graph에 대한 개념정리 - 2
Graph에 대한 개념정리 - 2
2021.05.21