Graph에 대한 개념정리 - 2
Spanning Tree
하나의 graph를 G라고 표현할 때, 우리는 Spanning Tree를 아래와 같이 정의할 수 있다.
G가 가지는 모든 Vertex를 연결하는 Cycle이 없는 Subgraph
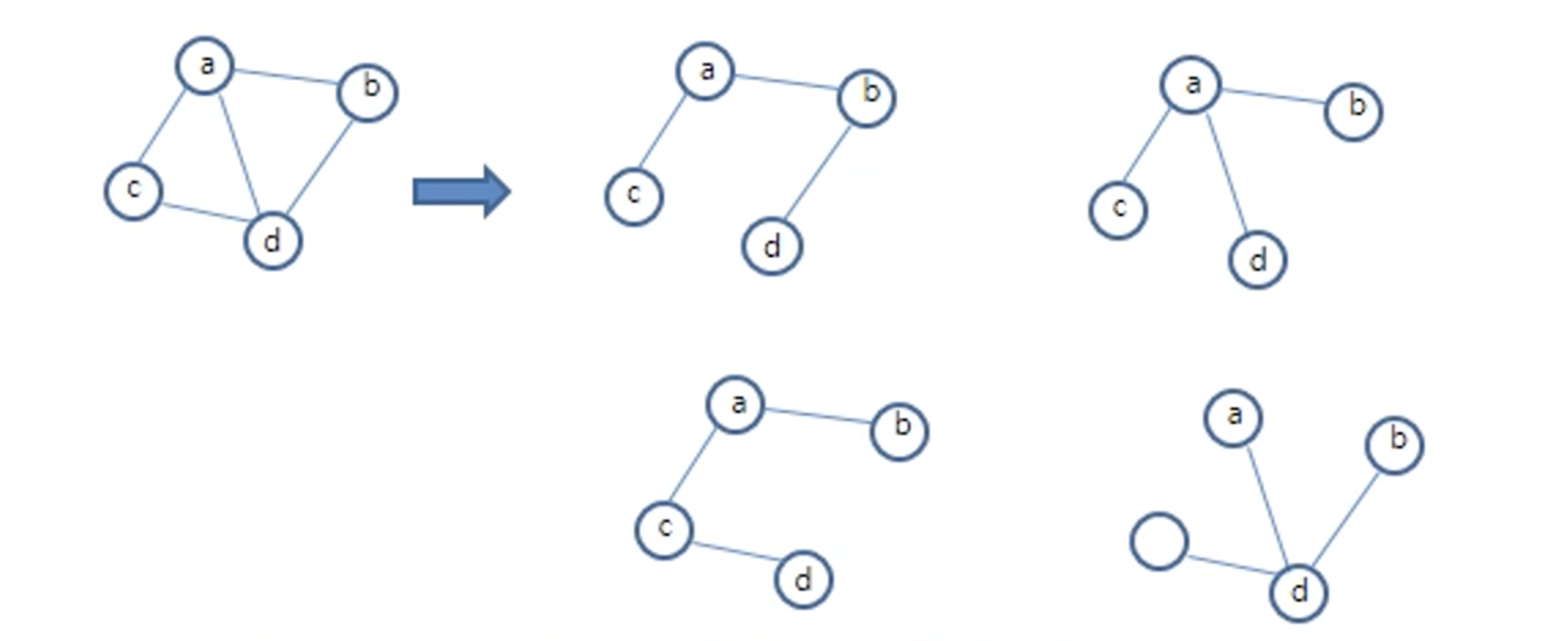
사실 Cycle이 존재하지 않는 Graph는 Tree로 볼 수도 있다. 그래서 이와 같이 graph를 다루고 있지만 Spanning Tree 라는 용어가 사용되는 것이다. 그래서 우리는 이 Spanning Tree에 약간의 제약조건을 부여함으로써 또 다른 이론이 만들어지기도 한다. 그래서 중복되는 edge가 없이 모든 vertex에 대해서 cycle 없이 연결이 이뤄져야 하기 때문에 n-1개의 edge를 가지게 된다.
BFS / DFS Spanning Trees
Spanning Tree의 종류에 대해서 다룰 때 우리가 어떤 Search의 과정을 통해서 얻게되는 Spanning Tree 들이 존재하는 데, 이에 대한 대표적인 Spanning Tree들이 바로 다음 두 가지 Tree 이다.
1. BFS Spanning Tree
2. DFS Spanning Tree

BFS Spanning Tree는 BFS의 과정을 통해서 얻어지게 되는 Spanning Tree를, DFS Spanning Tree는 DFS의 과정을 통해서 얻어지게 되는 Spanning Tree를 가리켜 말하는 것으로써, 이것은 Traverse 되는 순서를 가리켜서 보여주게 된다.
그래서 위와 같이 주어진 원래 그래프를 보고 이에 대한 BFS / DFS Spanning Tree를 그려낼 수 있으면 된다. 그렇기 때문에 이는 우리가 BFS, DFS에 대해서 정확히 이해했는 지를 확인해 볼 수 있는 하나의 좋은 수단이 될 수 있다.
이어서 Graph와 관련된 또 다른 용어의 정리를 살펴보도록 하겠다.
Biconnected Components
articulation point를 갖지 않는 connected graph
articulation point
해당 vertex를 삭제했을 때, 원 graph가 2개 이상의 biconnected graph로 분리되도록 하는 vertex

그래서 주어진 그래프를 보고 해당 graph가 articulation point를 가지는 지를 판별하고 이를 찾을 수 있도록 해당 개념을 이해하면 된다.
Minimum Cost Spanning Tree
Weighted Graph에서 Cost의 합이 최소인 Spanning Tree를 찾는 문제
왼쪽에 있는 Graph에 대한 Spanning Tree는 여러 종류가 있지만, 이 중에서 가장 최소비용에 해당하는 Spanning Tree를 찾는 것이 해당 주제에서의 논점이다.

이 문제를 해결하기 위해서 알고리즘으로 정형화된 것이 대표적으로 3가지가 알려져 있으며, 그 각각의 내용은 다음과 같다.
(각 알고리듬의 이름은 해당 알고리듬을 제안한 사람들의 이름을 딴 것이다.)
1. Kruskal's Algorithm
2. Prim's Algorithm
3. Sollin's Algorithm
1. Kruskal's Algorithm
전체 edge의 집합을 cost 순서로 sort하고, cost 순서대로 edge를 판단하여 적용
해당 알고리듬을 자연어로 기술해보면 다음과 같이 표현할 수 있다.
1. 전체 edge의 집합을 cost 순서로 sorting
2. cost 순서로 해당 edge가 cycle을 이루지 않는 경우 선택
3. 그는 (n-1)개의 edge가 선택될 때까지 이를 반복한다.
해당 알고리듬의 동작과정을 그림으로 표현해보면 다음과 같다.


2. Prim's Algorithm
start vertex에서 시작하여 현재 유지되고 있는 connected component와 연결된 edge를 고려
해당 알고리듬을 자연어로 기술해보면 다음과 같이 표현할 수 있다.
1. start vertex 로 부터 시작
2. 현재 구성되는 connected component와 (외부로) 연결된 edge 중에서 최소 cost edge를 선택
3. (n-1)개의 edge가 선택될 때 까지 다음을 반복한다.
해당 알고리듬의 동작과정을 그림으로 표현해보면 다음과 같다.


3. Sollin's Algorithm
해당 알고리듬은 이전에 제시했던 두 알고리듬에 비해서 비교적 최근에 제시된 알고리듬에 해당한다.
각 vertex를 개별 connected component로 고려하여 한 개씩 edge를 선택하여 추가
해당 알고리듬을 자연어로 기술해보면 다음과 같이 표현할 수 있다.
1. 각 vertex를 connected component 로 고려
2. 각 connected component에 대하여 최소 cost edge를 한 개씩 추가
3. 전체가 한 개의 connected component가 되면 종료
해당 알고리듬의 동작과정을 그림으로 표현해보면 다음과 같다.

'Computer Science > 알고리즘' 카테고리의 다른 글
| 유클리드 호제법 (Euclidean-algorithm) (0) | 2023.06.07 |
|---|---|
| Greedy Algorithm (0) | 2022.07.11 |
| Graph 에 대한 개념정리 - 4 (0) | 2021.05.22 |
| Graph에 대한 개념정리 - 3 (0) | 2021.05.21 |
| Graph에 대한 개념정리 - 1 (0) | 2021.05.21 |
댓글
이 글 공유하기
다른 글
-
Greedy Algorithm
Greedy Algorithm
2022.07.11 -
Graph 에 대한 개념정리 - 4
Graph 에 대한 개념정리 - 4
2021.05.22 -
Graph에 대한 개념정리 - 3
Graph에 대한 개념정리 - 3
2021.05.21 -
Graph에 대한 개념정리 - 1
Graph에 대한 개념정리 - 1
2021.05.21