Graph에 대한 개념정리 - 1
Graph
graph는 다음 두 가지 요소로 이루어진다.
1. Vertex의 집합
2. Edge의 집합
여기서 Vertex는 "어떤 대상의 객체"를 의미하고, Edge는 "Vertex간의 관계"를 뜻한다.

Graph와 관련된 용어정리
Graph와 관련되서 알고 있어야할 용어의 종류는 다음과 같다.
1. Vertex
2. Edge
3. Adjacent
4. Path
5. Length of a path
6. Connected
7. Connected Components
8. Cycle
Vertex
실세계에서의 어떤 대상을 표현하는 객체
문헌에 따라서 Vertex를 "node"라고 표현하기도 함.
Edge
Vertex 간의 관계
두 Vertex간에 관계가 존재하는 경우 Edge가 존재한다. 문헌에 따라서 Edge를 "arc"라고 표현하기도 한다.
Adjacent
두 Vertex 간에 Edge가 존재함을 의미
Path
두 Vertex간에 Edge로서 연결되는 Vertex의 Sequence
Length of a path
path를 구성하는 edge의 수
Connected
두 Vertex 간에 path가 존재함을 의미
path가 존재함을 의미이기 때문에 두 vertex간에 직접적인 연결뿐만 아니라 간접적인 연결이 존재하는 경우에 대해서도 포함된다.
Connected Components
상호 연결된 subgraph
Cycle
시작과 끝이 동일한 vertex인 path
Edge의 표기
1. (v1, v2) - 방향성이 없는 undirected graph, 우리가 일반적으로 말하는 graph에 해당
2. <v1, v2> - 방향성이 존재하는 directed graph, digraph 라고 표현하기도 함


실세계의 data를 표현할 때에는 방향성의 개념이 존재하기 때문에 directed graph의 개념이 존재한다.
Strongly Connected
Digraph에서 양방향 path를 가진 경우
Degree of Vertex
그 Vertex와 연결된 edge의 수
1. indegree - incoming (vertex 기준 들어오는 방향)
2. outdegree - outgoing (vertex 기준 나가는 방향)
Fully Connected Graph의 edge 수
n * (n-1) / 2
해당 문제는 서로 다른 2개의 vertex를 매칭하는 모든 경우의 수를 세는 것과 같은 문제이기 때문에 "n combination 2"로 해당 문제를 표현할 수 있다.
한붓 그리기
Graph에서는 각 vertex를 한 붓 그리기로 모두 처리할 수 있는 지에 대해서 알아볼 수 있는 데 이를 판단할 수 있는 조건이 존재한다. 아래의 조건을 만족하는 경우 해당 graph는 한붓 그리기가 가능하다.
graph 상에서 degree가 홀수인 vertex가 존재하지 않거나 2개인 경우
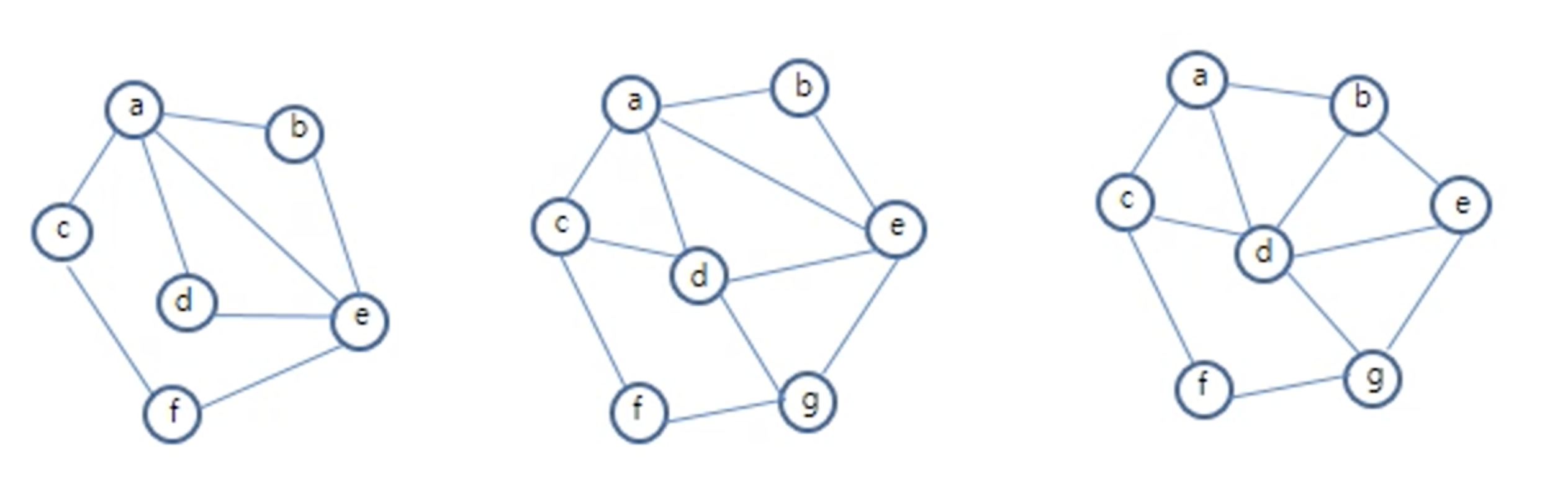
degree가 홀수인 vertex가 존재하지 않는 경우 graph 상의 어느 vertex에서 출발해도 한붓 그리기가 가능하며, degree가 홀수인 vertex가 2개인 경우에는 둘 중 하나에서 출발하여 나머지 하나로 도착하는 형식으로 한붓 그리기를 만족한다.
Graph Representation
우리는 시각적으로 그래프를 표현하는 것이 가능하지만, 실제 컴퓨터 상에서는 우리가 보는 것처럼 그래프를 그대로 표현하는 것이 불가능하다. 하지만 이러한 시각적인 그래프를 컴퓨터에서 내부적으로 표현하는 방법은 다음과 같은 방법들이 존재한다.
1. Adjacency Matrix
2. Adjacency List
Adjacency Matrix
1. 방향성이 없는 경우 (Graph)

위와 같이 각 vertex에 대한 정방형 2차원 배열을 생성하고, 각 vertex 별로 adjacent한 vertex에 대해서는 1을, 그렇지 않는 것에 대해서는 0을 할당한다. 위와 같이 방향성이 없는 Undirected Graph의 경우에는 대각선을 기준으로 대칭하게 해당 matrix가 나타나게 되서 이를 절반을 쪼깨도 무난하게 표현할 수 있다. 하지만 컴퓨터 내부적으로 삼각형 형태로 배열을 표현하는 것이 다소 어렵기 때문에 이러한 중복성을 가지고 있어도 그냥 정방향 2차원 배열을 사용해서 표현하는 것이 일반적이다.
2. 방향성이 존재하는 경우 (Digraph)

방향성이 존재하는 Graph를 adjacency matrix로 표현하는 경우에는 한쪽을 to, 나머지 한쪽을 From으로 설정하고 이렇게 해서 해당 방향에 대해서 adjacency가 존재하는 경우 1을, 존재하지 않는 경우 0을 할당하는 방식으로 matrix에 값을 할당한다. 만약 가로를 to로 세로를 From으로 할당하게 되면 matrix의 column은 outdegree를, row는 indegree를 의미하게 된다.
따라서, 방향성이 없는 Graph를 adjacent matrix로 표현하는 경우에는 matrix에서의 행과 열의 의미가 서로 동일하지만, 방향성이 존재하는 graph의 경우에는 행과 열의 의미가 서로 다르고 이 각각을 어떻게 설정하느냐에 따라서 matix에 값이 할당되는 양상도 달라짐을 같이 기억해두도록 하자.
Adjacent List
adjacent list의 경우 각 vertex에 대해서 adjacent한 다른 vertex들을 linked list의 형태로서 표현하는 것이 특징이다. 이전에 2차원 배열을 사용해서 표현하는 adjacent matrix 방식에 비해서 오직 1인 값들에 대해서 Linked list로 다루기 때문에 memory space 활용 측면에서 Adjacent Matrix 방식에 비해서 더 효율적이라고 볼 수 있다.

A weighted graph
이전까지 살펴본 예시에서는 각 vertex간에 edge를 통해서 "connected" 된다는 사실에만 집중했지만, 아래와 같이 각 edge에 대해서 "가중치(weight)"의 개념을 도입하는 할 수 있다. 이러한 weighted graph는 두 경로 사이에 최단 경로를 찾거나 최저비용의 경로를 탐색할 때 각 edge에 가중치를 할당하고 이를 기반으로 탐색을 진행함으로서 가장 효율적인 결론을 도출하는 데 유용하게 활용될 수 있다. Weighted Graph는 아래와 같이 Adjacent Matrix의 형태로 동일하게 표현할 수 있다.

Graph의 연산(BFS, DFS)
Graph에도 연산이라는 개념이 존재한다. Tree에서 Traversal 이라는 주제에 대해서 다뤘던 것처럼 graph에서도 각 vertex를 경로의 중첩없이 모든 vertex를 탐색하도록 하는 "Search"라는 개념이 연산이 존재하며, 이를 수행할 수 있는 알고리듬으로서 대표적으로 BFS와 DFS가 존재한다. 그렇다면 각각의 알고리듬들에 대해서 생각해보도록 하자.
DFS (= Depth First Search)
DFS는 Depth First Seach의 약자로서 Grpah를 깊이 우선적으로 탐색하는 것을 말한다. 그래서 하나의 start vertex를 기준으로 그 깊이를 우선적으로 각 vertex를 탐색하고, 해당 path에 대해서 더 이상 탐색할 vertex가 존재하지 않는 경우 Back tracking 하여 다른 경우데 대해서 depth 기준으로 동일하게 탐색을 진행한다.
그렇다면 DFS의 알고리듬을 기술해보도록 하겠다. 여기서는 코드 수준이 아닌 자연어 수준에서 알고리듬을 기술할 것이다.
단, 여기서 해당 알고리듬을 적용함에 있어 임의의로 선정하여 지정되는 "start vertex"가 존재함을 가정한다.
1. start vertex에 대한 처리를 수행하고, 이를 stack에 넣는다.
2. stack이 empty가 될 때까지 다음을 반복한다.
- stack의 top 원소와 adjacent한 vertex 중에 아직 방문하지 않은 vertex 1개를 선택하여 처리 후 이를 stack에 넣는다.
- 더 이상 선택할 원소가 없는 경우, stack에서 원소 1개를 pop한다. (Back Tracking)
(여기서 말하는 "처리"는 사용자가 정의하는 바에 따라 달라질 수 있다. 단순히 해당 vertex에 대한 정보를 출력하는 것일 수도, 해당 vertex의 정보를 사용하여 또 다른 알고리듬을 실행하는 루틴으로 이어질 수도 있는 등 사용자 정의에 따라서 다양한 표현으로 연결될 수 있는 표현임을 기억하도록 하자.)
BFS (= Breadth First Seach)
BFS는 Breadth First Seach의 약자로서 Graph를 너비 우선적으로 탐색하는 것을 말한다. 그래서 하나의 start vertex를 기준으로 adjacent vertex들을 모두 탐색한 후 또 다시 그 각각의 vertex들의 adjacent vertex를 탐색하는 방식으로 탐색이 이루어지게 된다. DFS와 비교했을 때 먼저 깊이 파고드는 것이 아니라 폭넓게 모든 case를 따져보고 있다는 점에서 그 차이가 있다고 할 수 있다.
그렇다면 DFS의 알고리듬을 기술해보도록 하겠다. 여기서는 코드 수준이 아닌 자연어 수준에서 알고리듬을 기술할 것이다.
단, 여기서 해당 알고리듬을 적용함에 있어 임의의로 선정하여 지정되는 "start vertex"가 존재함을 가정한다.
1. start vertex에 대한 처리를 수행하고, 이를 queue에 넣는다.
2. queue가 empty가 될 때까지 다음을 반복한다.
- stack의 front 원소와 adjacent한 vertex 중에 아직 방문하지 않은 vertex 1개를 선택하여 처리 후 이를 queue에 넣는다.
- 더 이상 선택할 원소가 없는 경우, queue에서 원소 1개를 delete한다.
'Computer Science > 알고리즘' 카테고리의 다른 글
| 유클리드 호제법 (Euclidean-algorithm) (0) | 2023.06.07 |
|---|---|
| Greedy Algorithm (0) | 2022.07.11 |
| Graph 에 대한 개념정리 - 4 (0) | 2021.05.22 |
| Graph에 대한 개념정리 - 3 (0) | 2021.05.21 |
| Graph에 대한 개념정리 - 2 (0) | 2021.05.21 |
댓글
이 글 공유하기
다른 글
-
Greedy Algorithm
Greedy Algorithm
2022.07.11 -
Graph 에 대한 개념정리 - 4
Graph 에 대한 개념정리 - 4
2021.05.22 -
Graph에 대한 개념정리 - 3
Graph에 대한 개념정리 - 3
2021.05.21 -
Graph에 대한 개념정리 - 2
Graph에 대한 개념정리 - 2
2021.05.21